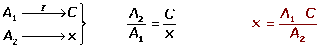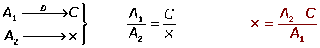PROFE RICHARD

1. Simbología Matemática 2. Números 3. Operatoria con los números reales     mínimo común múltiplo y máximo común divisor         3.1 Problemas y ejercicios de aplicación "mcm y MCD" 4. Jerarquía de las operaciones 5. Antecedentes sobre fracciones         5.1 Sumas y restas               5.2 Multiplicación y división         5.3 Ejercicios de fracciones         5.4 Solución de ejercicios de fracciones 6. Proporcionalidad         6.1 Regla de 3 simple         6.2 Regla de 3 inversa         6.3 Regla de 3 compuesta         6.4 Ejercicios de proporcionalidad 7. Potenciación y radicación 8. Lenguaje algebraico          8.1 Ejercicios de lenguaje algebraico 9. Sumas y restas algebraicas 10. Apendice          10.1 Serie de Fibonacci         10.2 Habilidad matemática parte 1         10.3 Habilidad matemática parte 2

Enuncia verbalmente las siguientes expresiones algebraicas: 1.    x - 2 : "La diferencia entre un número y 2" 2.    2x 3.    x + 3 4.    2x + 5 5.     x - 3y 6.    x+y        x-y    Expresa algebraicamente los siguientes enunciados verbales:   1.    Un número cualquiera.   2.    El doble de un número cualquiera.   3.    Un número aumentado en 5.   4.    Un número disminuido en 3.   5.    La quinta parte de un número.   6.    El doble de un número aumentado en 4   7.    El triple de un número disminuido en 5.   8.    El doble de la suma de dos números   9.    La mitad de la diferencia de dos números 10.    El triple del cuadrado de la suma de dos números. Resuelve los siguientes problemas de enunciado verbal: 1) Si al doble de cierto número se suma 6, el resultado es 4 unidades menos que el triple del número. ¿Cuál es el número? 2)Encontrar el número cuya sexta parte más su novena parte es 15. 3)La suma de tres núme

Regla importante:  solamente los términos semejantes se pueden sumar o restar Términos semejantes son los que tienen exactamente la  misma parte literal , es decirlas mismas letras y cada una con los  mismos exponentes. Procedimiento: Se agrupan los términos semejantes Se suman o restan los coeficientes (parte numérica) Luego se escribe la parte literal, anteponiendo el signo resultante. Ejemplos: 1)  25x + 12x - 31x - 8x +5x = 3x 25 + 12 - 31 - 8 +5 = 3 2)  43mx³ + 7mx³ - 17mx³ - 13mx³ = 20mx³ 43 + 7 - 17 - 13 = 20 3)   4 x +  2 x -  5 x +  7 x +  x  =  79 x 3 5 2 4 3 60 4  +  2  -  5  +  7  +  1  =  79 3 5 2 4 3 60 Tal como se observa no es diferente de una suma ordinaria. Variación: cuando en la expresión no todos los términos son semejantes se suman solo los términos semejantes y se dejan indicado el resto: Ejemplos: 1) 25x + 12y - 31x - 8y +5x = 4y- x Para las x: 25 – 31 + 5 = -1 para las y: 12 – 8 = 4 2) 43mx³ + 7mx - 17mx³ - 13mx = 26

El lenguaje que usamos en operaciones aritméticas en las que sólo intervienen números se llama  lenguaje numérico . En ocasiones empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico. El lenguaje que utiliza letras en combinación con números y signos, y, además, las trata como números en operaciones y propiedades, se llama  lenguaje algebraico . La parte de las Matemáticas que estudia la relación entre números, letras y signos se llama  Álgebra . Características del lenguaje algebraico 1.- El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve. El conjunto de los múltiplos de 5 es 5 • = {±5, ±10, ±15, ...}. En lenguaje algebraico se expresa 5 •  n , con  n  un número entero. 2.- El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter ge

Potenciación y Radicación Potencias Esencialmente una potencia nos representa una multiplicación por sigo mismo de un número que llamamos “base”, tantas veces como lo indique otro número que llamamos “exponente”. Raíces Las raíces son casos más generales de las potencias, ya que corresponden a una potencia, pero de índice racional. Decimos que una raíz n-ésima de un número a es b, si y solo si la n-ésima potencia de b es a, es decir: Regresa al temario

La  regla de tres compuesta  se emplea cuando se relacionan  tres o más magnitudes , de modo que a partir de las relaciones establecidas entre las magnitudes conocidas obtenemos la desconocida. Una  regla de tres compuesta  se compone de varias  reglas de tres simples  aplicadas sucesivamente. Como entre las magnitudes se pueden establecer relaciones de  proporcionalidad directa o inversa , podemos distinguir  tres casos  de regla de tres compuesta : Regla de tres compuesta directa Ejemplo: Nueve grifos abiertos durante 10 horas diarias han consumido una cantidad de agua por valor de 20 €. Averiguar el precio del vertido de 15 grifos abiertos 12 horas durante los mismos días. A  más  grifos,  más  euros    Directa . A  más  horas,  más  euros    Directa . 9 grifos    10 horas   20 € 15 grifos   12 horas      x € Regla de tres compuesta inversa 5 obreros trabajando, trabajando 6 horas diarias construyen un muro en 2 días. ¿Cuánto tardarán 4 obreros traba

Consiste en que dadas dos cantidades correspondientes a magnitudes inversamente proporcionales, calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud. La  regla de tres inversa  la aplicaremos cuando entre las magnitudes se establecen las relaciones: A  más    menos . A  menos    más . Ejemplos Un grifo que mana 18 l de agua por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 l por minuto? Son magnitudes  inversamente proporcionales , ya que  a menos  litros por minuto tardará  más  en llenar el depósito . 18 l/min   14 h 7 l/min        x h 3 obreros construyen un muro en 12 horas, ¿cuánto tardarán en construirlo 6 obreros? Son magnitudes  inversamente proporcionales , ya que a  más  obreros tardarán   menos  horas . 3 obreros    12 h 6 obreros        x h Regresa al temario

Consiste en que dadas dos cantidades correspondientes a magnitudes  directamente proporcionales , calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud. La  regla de tres directa  la aplicaremos cuando entre las magnitudes se establecen las relaciones: A  más     más . A  menos     menos . ejemplos:   Un automóvil recorre 240 km en 3 horas. ¿Cuántos kilómetros habrá recorrido en 2 horas? Son magnitudes  directamente proporcionales , ya que  a menos  horas recorrerá  menos  kilómetros. 240 km  3 h x   km    2 h Ana compra 5 kg de patatas, si 2 kg cuestan 0.80 €, ¿cuánto pagará Ana? Son magnitudes  directamente proporcionales , ya que  a más  kilos,  más  euros. 2 kg  0.80 € 5 kg   x € Regresa al temario